In our previous blog post on DLC (Discreet Log Contracts), we discussed the essential cryptographic primitive required, which is a verifiable witness encryption scheme. However, it's important to note that the evolution of this concept was not a straightforward process and involved the collaborative efforts of many individuals, starting with Dryja's original application idea.

In this post, we begin by explaining the process of utilizing a private key as a decryption key for signature, thereby transforming it into a trigger for a transaction. This leads us to delve into the concept of adaptor signatures, specifically in the context of Schnorr's signature for the sake of simplicity. Subsequently, we delve into the definition of an oracle attestation, enabling efficient communication of which private key will be revealed based on the attested event.

Finally, we present the three main proposal protocols for DLC (Discreet Log Contracts). We start with an overview of Dryja's original proposal, followed by the current proposal that incorporates adaptor signatures. Additionally, we present the most ambitious proposal, known as ObC payments (Oracle-Based Conditional payments), developed by Llyold Fournier. ObC payments leverages a truly verifiable witness encryption, optimizing efficiency through the interaction between BLS signatures, identity-based encryption of Schnorr's signature.

This post will be technical, there will be maths! Do you have time ahead to focus? If yes, then grab your mug of tea or coffee and enjoy the ride!

Attestation as a decryption key

Verifiability with naive symmetric encryption

In our previous post, we discussed the concept of utilizing an oracle attestation, specifically Olivia, to enable Alice and Bob to decrypt the exchanged signature. This decryption would be applicable only to the payout associated with a signed event, allowing one of them to unilaterally execute the contract and claim their respective gain.

One straightforward and simplistic approach would involve Alice and Bob encrypting their Conditional Execution Transaction (CET) signatures with Olivia's corresponding signature before transmitting them to each other. However, this approach assumes that both Alice and Bob possess the same signature derived from Olivia's private key, without any involvement from Olivia. As a result, both parties would already be able to decrypt the counterpart's signature, rendering the process meaningless.

One crucial aspect missing from this scheme is what is known as "one-wayness." It is essential that Alice and Bob can encrypt a signature, but it must be computationally infeasible for the other party to reverse-engineer or recover the original signature from the encrypted version without assistance from Olivia.

One-wayness with asymmetric encryption: DLC literally

A more sophisticated approach is to utilize asymmetric key encryption for the signature. Alice and Bob can agree on a private key while knowing the corresponding public key, which they can use to encrypt their signatures. However, neither of them would have the ability to decrypt the ciphertext exchanged between them without the private key. One well-known algorithm that facilitates such encryption using elliptic curves is ElGamal encryption.

Olivia could potentially agree to disclose her private key when attesting to an event, enabling Alice and Bob to decrypt the exchanged signatures. As the name "Discreet Log Contract" implies, Alice and Bob need to learn the discrete logarithm of something in order to settle (the private key of a point represents the discrete logarithm, while the public key of a scalar involves modular exponentiation). However, using the same key to encrypt all the CET's signatures would be problematic, as any of them could be decrypted to claim funds regardless of Olivia's attestation. In this case, Olivia would need to announce all the possible outcomes she may attest and specify which public key corresponds to the one revealed for each outcome.

Unfortunately, this approach still falls short as it lacks verifiability despite being one-way. Asymmetric key encryption algorithms like ElGamal inherently require the encrypted message to be represented in a specific mathematical object's constrained format, such as the x-coordinate of an elliptic curve point in the case of ElGamal. While this is suitable in a hybrid cryptosystem where the encrypted message serves as a random key for decrypting a larger message encrypted symmetrically, it doesn't provide an intuitive way for Alice and Bob to verify that the encrypted message is indeed a signature.

Adaptor signature

Initially, finding a solution that allows for encrypting a signature in a way that the counterparty can verify its validity without knowing the actual signature may seem like a magical concept. However, instead of encrypting the signature after Alice and Bob produce it, they can modify the signature protocol itself to generate a type of partial signature. This partial signature is not valid on its own but can become valid when combined with a specific private key belonging to Olivia. This approach is known as an "adaptor signature." While it is simpler to explain the concept of adaptor signatures in the context of Schnorr signatures, it is worth noting that it is also possible to define an adaptor signature protocol for ECDSA signatures.

Let's review some fundamental concepts: The primary objective of Bob's signature is to provide public proof that he possesses the private key corresponding to his public key, B. To achieve this without revealing his actual private key, Bob will demonstrate his knowledge of both the private key of his public key and another randomly chosen private key simultaneously. Bob initiates this process by selecting a random scalar value \( r_{Bob} \) called nonce secret, computes and reveals its public key called nonce \( R_{Bob} = r_{Bob} G \). This is called the commitment step.

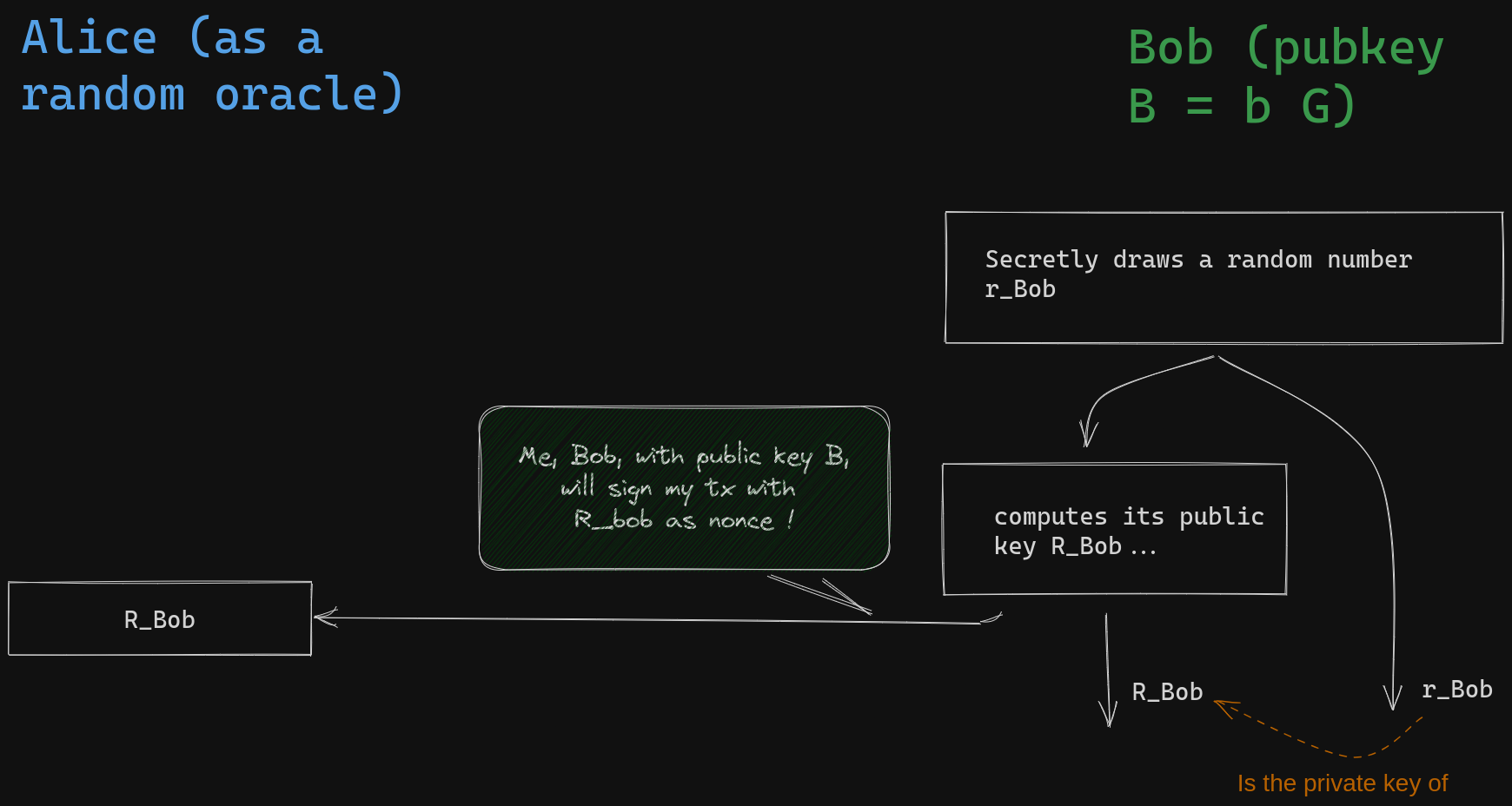
Next, Bob must reveal the private key of a derived public key that is obtained through a linear combination of his public key and the nonce public key he committed to using. The coefficient of this combination is precisely determined by the message being signed and the nonce he committed to (it is the hash of their concatenation plus Bob's public key, \(B\)). This is called the challenge step.

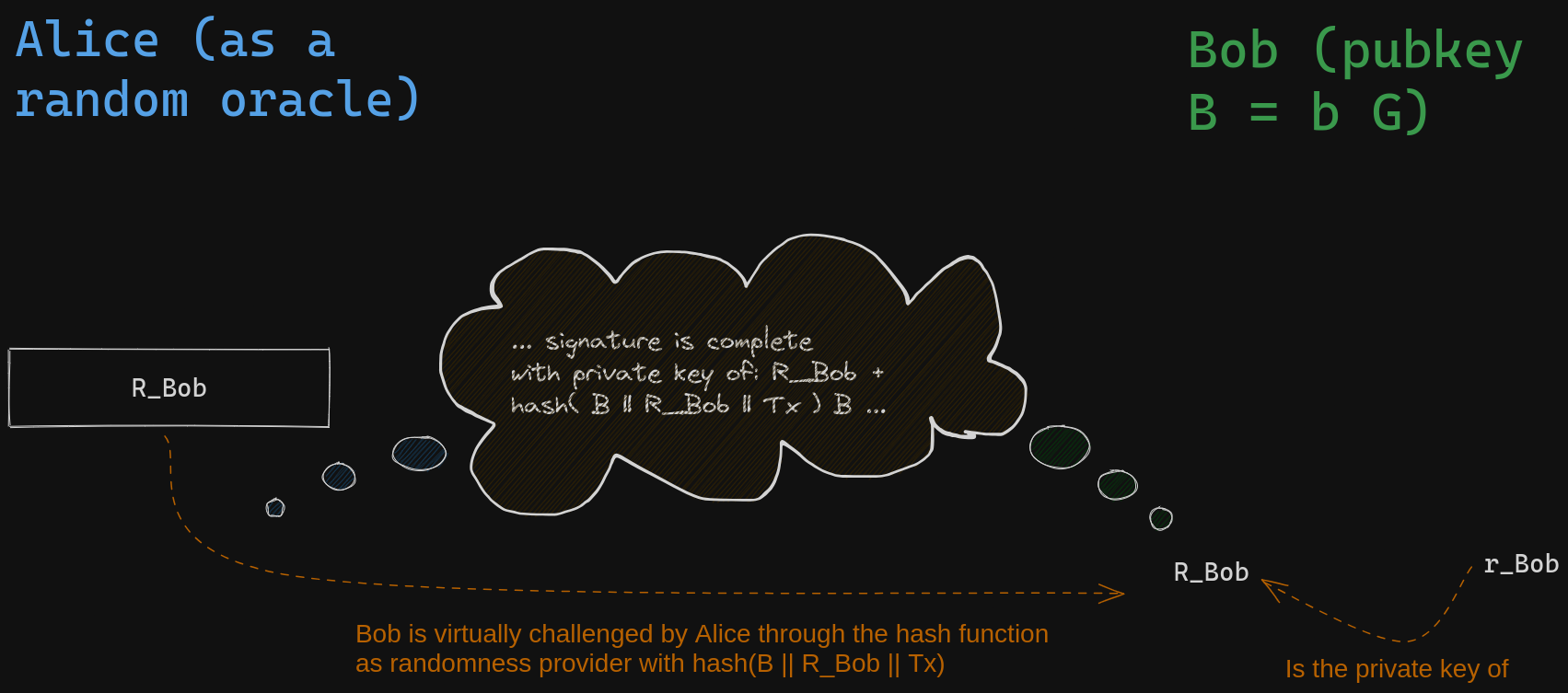
Bob achieves this by performing the same combination using private keys instead of public keys, leveraging the mathematical linearity of associating public keys with private keys. Anyone can verify the validity of the result.

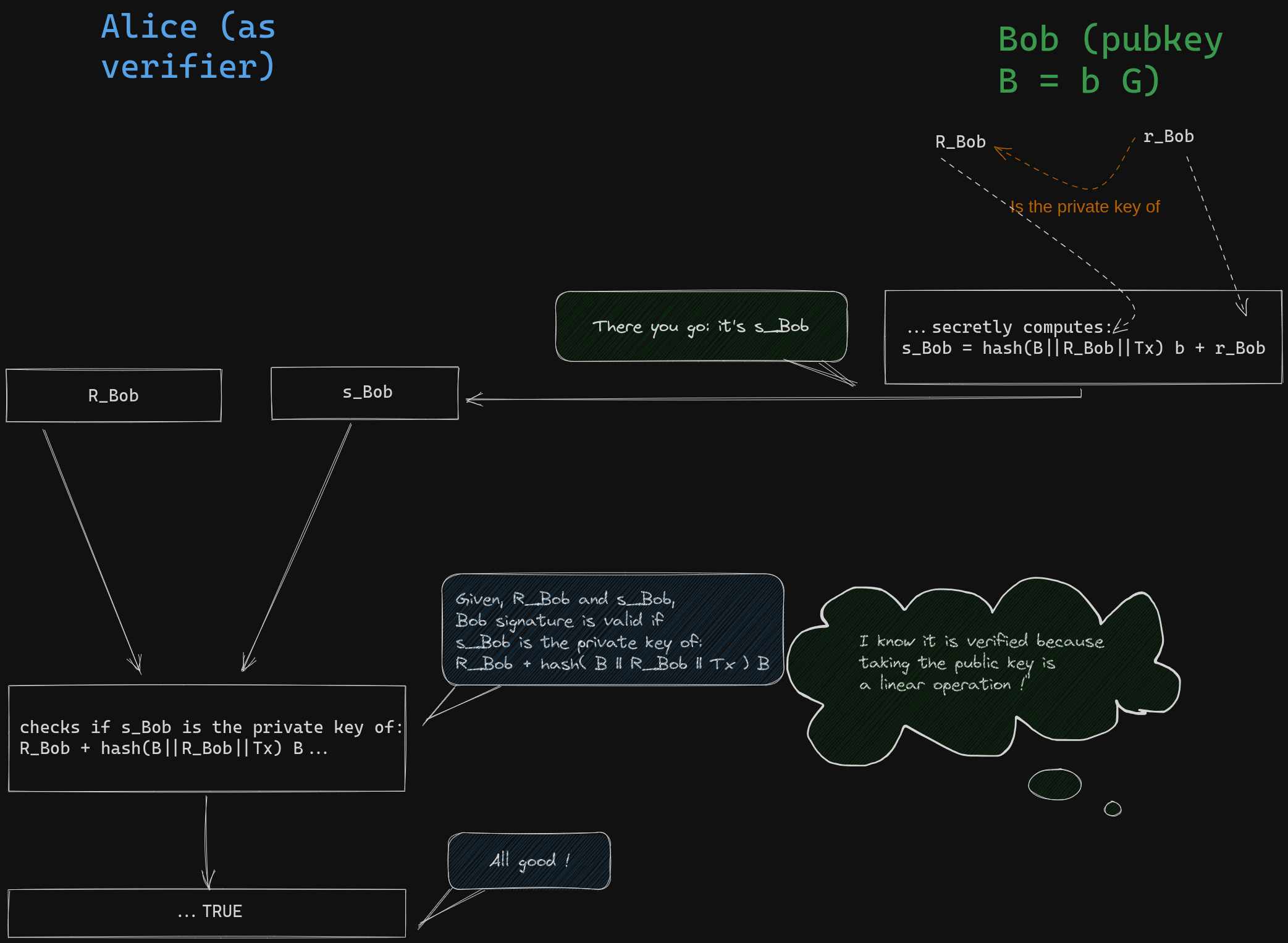
The core insight behind Adaptor signatures is the dual use of the nonce secret in a typical signature process: once to calculate the nonce and once to derive the disclosed private key. In the case of an adaptor Schnorr signature, the nonce public key is modified by another public key while keeping the nonce secret unchanged. This modification renders the signature invalid, but it can be easily verified that the missing secret value needed to make it valid corresponds to the private key of the modified public key. To illustrate this, let's consider how Bob can construct an adaptor signature for Alice, enabling her to claim his funds using the potential revealed private key of Olivia, \(s_{Azure}\), if the Azure team emerges as the winner.

Bob, without knowledge of \(s_{Azure}\), can generate an adaptor signature that Alice can verify. This is possible because Olivia has already announced her intention to disclose the private key of \(S_{Azure} = s_{Azure} G\) if Azure wins. Bob initiates the signature protocol by following the standard procedure, using a random source to obtain a secret nonce scalar value \( r_{Bob} \). He then calculates the corresponding public nonce \( R_{Bob} = r_{Bob} G \), which he intends to use for the signing process.

In a typical Schnorr signature, Bob would calculate the designated coefficient for the combination, which involves appending the transaction payload to the coordinates of the nonce point, hashing the result, multiplying it by his private key, and finally adding \( r_{Bob} \). He would then share the resulting pair, along with the nonce point \( R_{Bob} \). Anyone could verify that the second component of the pair corresponds to the private key of \(R_{Bob} + hash(B || R_{Bob} || Tx ) B \):

\[ (R_{Bob}, r_{Bob} + b \times hash(B || R_{Bob} || Tx ) )\]

However, Bob doesn't want his signature to be valid immediately. Before following the previously described process, Bob will add \(S_{Azure}\) to his nonce public key and perform the same calculations without modifying the secret nonce.

The virtual verifier, represented by the hash function, understands is that Bob will produce a valid signature using the nonce \(R'_{Bob}\) and challenge him accordingly. It is expected that Bob will reveal the private key of a public key that can be already computed from the tweaked nonce:

Bob can not compute the required private key without knowing \(s_{Azure}\), but he will do the same computation as typical schnorr signature using the secret a draw for the nonce, the nonce send to Alice and his private key. As a result, the "signature" he will provide to Alice will appear as this pair of values:

\[ \begin{align*} R'_{Bob} &= &R_{Bob} + S_{Azure} \\ s_{Bob} &= &r_{Bob} + b \times hash(B || R'_{Bob} || Tx ) \end{align*} \]

This is an invalid signature due to a mismatch between the secret nonce \( r_{Bob} \) and its corresponding public key \(R'_{Bob} = R_{Bob} + S_{Azure}\) in the hash function. However, Alice can independently verify that the mismatch causing the signature to be invalid is EXACTLY \(S_{Azure} \) . In fact, if we attempt to verify the signature, we calculate the public key or \(s_{Bob}\) as follows:

\[ \begin{align*} & s_{Bob} G \\ = & r_{Bob} G + hash(B || R'_{Bob} || Tx) \times b G \\ = & R_{Bob} + hash(B || R'_{Bob} || Tx) B \\ = & R'_{Bob} +hash(B || R'_{Bob} || Tx) B - S_{Azure} \end{align*} \]

Alice can verify that adding \(S_{Azure}\) is the correct adjustment to the verification equation in order for Bob's signature to be valid with the modified nonce \(R'_{Bob}\). This serves as proof to Alice that if she knows \(s_{Azure}\), by adding it to the scalar component \(s'_{Bob-CET_ {Azure}} \) of Bob's adaptor signature, she will obtain a valid Bob's signature. With this valid signature, Alice can then use it to claim the funds based on the content of the Conditional Execution Transaction (CET) in the case where Azures win. This implies that if Olivia reveals the private key of \(S_{Azure}\), Alice will have the ability to execute the contract with Bob by obtaining Olivia's attestation and broadcasting a valid transaction to claim the funds!

This initial setup is promising, but it presents a challenge as Olivia would need to generate and securely store a private key for each potential outcome between the announcement and attestation. Now, let's explore how we can scale Olivia's capabilities to accommodate a larger number of outcomes.

Oracle's keys derivation

"One key, One outcome" approach

The approach described above presents challenges for Olivia, as she needs to announce a public key for each possible outcome she may attest. This can be difficult for Olivia to manage, as she must ensure the private keys are kept secure and only reveal the one associated with the attested outcome. This requires Olivia to maintain stateful storage of critical data between the announcement and attestation periods.

Additionally, this approach incurs a cost for Olivia's users. Each potential outcome requires an adaptor signature exchange, which may be feasible for events with a small number of cases, but becomes impractical for numerical outcomes with a large range. This results in users having to encrypt the same CET's signature multiple times if the payout covers a wide range of values. Olivia could adjust the range of outcomes she signs, but this would limit the use cases for her attestations or require users to inform Olivia about their specific contracts, compromising protocol privacy.

While this setup may not be suitable for trading with DLC, it offers several advantages. One significant advantage is that it is easy for Alice and Bob to use a federation of oracles that employ this signing method. They could non-interactively aggregate the public keys of oracles and their signatures using a FROST construction to privately set up a threshold federation of oracles. However, they need to be cautious, as Alice could choose oracles that collide in an unexpected way, allowing her to claim funds for outcomes other than the ones effectively attested. This is known as a Wagner's attack or birthday attack.

A possible improvement to scale Olivia's oracle system would be to establish a secure method for deriving all the public keys associated with each outcome. This would allow Olivia to announce a small and easily broadcasted set of public keys, and she could compute only the private key associated with the attested outcome during the attestation process, without the need to compute the others.

Naive BIP32 derivation of public keys

Bitcoiners are familiar with deriving public keys from other public keys using the BIP32 standard. BIP32 introduces a key derivation process where a seed is split into a private key and a chaincode, collectively referred to as an XPRV. Corresponding to each XPRV is an XPUB, which is essentially the same as the XPRV but with the private key replaced by its public key. When derivation is not hardened, it becomes possible to derive all the public keys associated with the private key derived from the XPRV using only the XPUB. This suggests that Olivia could announce an XPUB instead of multiple public keys and specify the derivation method everyone should use to obtain the private key she will reveal during attestation. Users can also employ the same XPUB child public key derivation.

However, this simplistic approach is not viable. While XPUB allows such derivation, it comes with the drawback that anyone who learns the private key of a derived key can trace it back to the parent key and subsequently derive all child private keys. This means that if Olivia reveals a private key to attest to an event, it enables anyone to compute the private key associated with any other event, which undermines the intended use case.

In the introduction paper on Discreet Log Contracts (DLCs) by Tadge Dryja, he proposed an innovative method to derive oracle's public keys that ensures revealing one of their private keys does not compromise the corresponding oracle public key. His approach to achieve this derivation was both simple and clever: the revealed private key is just the second component of a Schnorr signature.

Schnorr Signature as a child public key derivation

Let suppose that to attest an event, Olivia will produce a schnorr signature of the outcome for her public key \(O\).

Looking at the verification equation of schnorr signature, Olivia's signature \( s_{Azure} \) of the winner "Azure" with the announcement nounce R and her public key \( O \) verifies the following equation:

\[ s_{Azure} G = R + Hash(O || R || "Azure") O \]

This equation exactly means:

\(s_{Azure}\) is the private key of \( R + hash(O || R||"Azure") O \) seen as a public key.

A fundamental property of a signature scheme is that the signature can only be produced by the owner of the private key associated with the public key. This is because the signature reveals the private key of a point, which is a binding combination of the public key and a one-time use public key R called nonce drawn by the signer. Dryja's idea is simple: by pre-announcing the nonce he will use to sign the event attestation, the oracle commits to revealing the private key of a public key that anyone can already derive. Thus, the verification point of the Schnorr signature can be used to set up a contract that is settled only if its discrete logarithm is revealed, indicating that the attested outcome matches the execution of the contract.

Unlike BIP32, the revelation of this private key does not leak the private keys of other outcomes. This is because the oracle did not reveal a chaincode attached to its public key, but just another public key: the nonce R. Furthermore, it is possible to create fraud proofs for oracles in some cases. If the oracle attests to two different outcomes with the same nonce, anyone can derive the oracle's private key and prove that the oracle can no longer be trusted.

An improvement of this child key derivation is that we do not actually need to use the same hashed data as in the Schnorr signature case. The entire hash in the signature can be replaced with any function that associates an index with an outcome. This makes the scheme insecure for signature purposes but still secure for deriving oracle public keys. If the nonce and public key of the oracle are removed from the hash digest, all oracles use the same index for a given outcome message. This allows for the non-interactive aggregation of oracle attestations as needed (with the caveat that security reduction may be affected due to a potential Wagner's attack).

Now that we understand the two core components of a DLC setup, we can review the various proposals and the current state of the art.

State of various DLC proposals

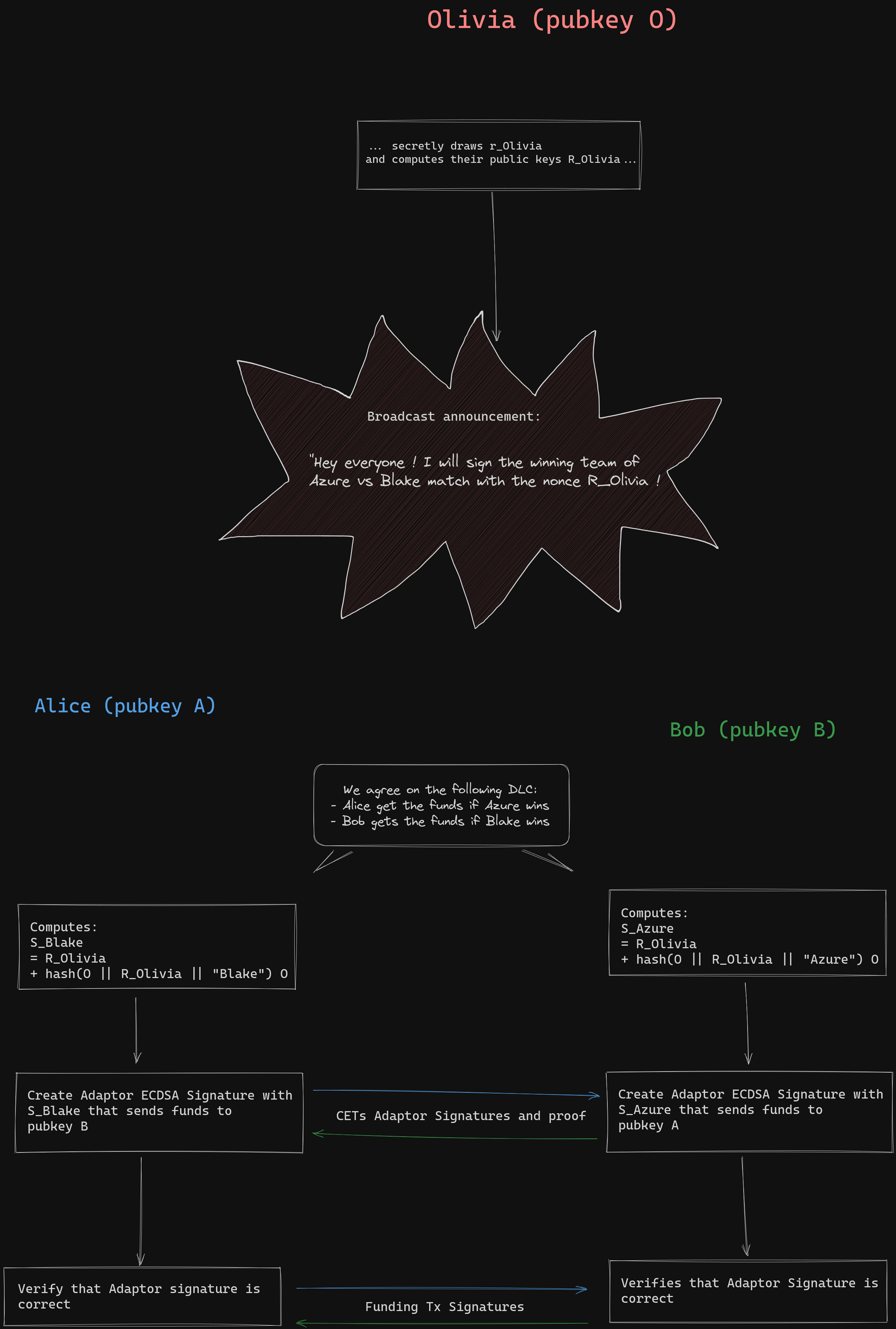
Dryja's original proposal

Original Dryja's proposal did not use adaptor signature or verifiable witness encryption. When presigning the CETs, Bob simply sign it normally but instead of sending the funds to Alice public key directly, Bob just send them to the sum of Alice public key with the derived key from the oracle. Alice public key is tweaked and Alice can check that she must sign for a new tweaked key \(\hat{A}^{Azure}\) :

\[\hat{A}^{Azure} = A + (R + hash(O || R || "Azure") O) \]

When Olivia signs that "Azure" to attest they are the winning team, Alice can compute the discreet logarithm of \(\hat{A}^{Azure}\) by just adding her private key to the value revealed by Olivia, hence the name "Discreet Log Contract":

\[ \hat{a}^{Azure} = a + s_{Azure} \]

Alice can then claim the fund with a last transaction. If Alice misused and broadcast the wrong Bob presigned transactions, she will not be able to claim them and Bob can claim them after a time lock expiration.

A simplified example of DLC funding according to this protocol is shown in the following image:

Dryja's initial design for DLCs was the first iteration of the concept. However, it lacked verifiable encryption and required an additional transaction to claim funds after the confirmation of the CET. This approach had limitations because on-chain transactions did not reveal the oracle signature. It became challenging to publicly prove that the oracle signed the event twice with different outcomes. Additionally, a presigned CET was required for each possible message the oracle would sign, even if they resulted in the same payout, due to the tweaking of public keys with each outcome. In contrast, when using adaptor signatures or verifiable witness encryption, it is possible to encrypt the same CET signature multiple times with different keys corresponding to outcomes with the same payout.

Adaptor signature for ECDSA

In the current specification, DLCs no longer use Dryja's public key tweaking, but instead employ an adaptor signature scheme. The proposed specification suggests using the classical Schnorr signature to derive keys from the oracle announcement, which are then used to create adaptor signatures for ECDSA.

It is not possible for the oracle to use ECDSA as key derivation. This is because ECDSA signature algorithm is somewhat reversed when compared to Schnorr: the signer proves his knowledge of the private key by revealing a combination of his public key and a public key computed from the message that gives the nonce. This means we do not know before the signature which private key will be revealed (through the coefficient of the combination).

Although it is not possible for the oracle to use ECDSA as key derivation, an adaptor signature scheme for ECDSA can be defined, allowing contracting parties to use ECDSA-based signatures. The DLC specifications currently specify an ECDSA adaptor signature protocol as a verifiable witness encryption scheme. The details of the ECDSA adaptor signature are more complex and can be found in the DLC specification repository. Notably, adaptor signatures with ECDSA require another cryptographic primitive called Proof of Discrete Logarithm Equivalence, which is already used in JoinMarket to prevent spam. With the adoption of Taproot, a specification for adaptor signatures for Schnorr signatures may be developed.

Other verifiable witness encryption schemes

The previously described schemes used Schnorr signatures for oracles. However, it is possible to construct different verifiable witness encryption schemes for DLCs. Originally, verifiable witness encryption does not assume knowledge of the signature's nonce. In the 1990s, Garg et al. proposed a generic approach where decryption is possible with any solution to a given puzzle. In this context, the oracle signature is seen as a valid solution to a puzzle, which would be finding a point and a scalar that satisfy the Schnorr signature's verification equation. Unfortunately, this approach is challenging to scale for practical DLCs.

One of the most ambitious proposals for verifiable witness encryption in DLCs is the one presented in an article by Lloyd Fournier. It allows oracles to use BLS signatures to attest to outcomes while contracting parties use Schnorr signatures. BLS signatures utilize elliptic curve pairings to produce signatures. However, supporting a known elliptic curve with such pairings, which is not the case for secp256k1 used in Bitcoin, is required.The main property of pairing is called bi-linearity: it allows to mathematical define "a product of any two points on the curve".

In the proposed approach by Madathil et al., the oracle's BLS signatures are reinterpreted as private keys for identity-based encryption that also utilizes pairings. The idea is to symmetrically encrypt the same CET signature multiple times with random scalars that are then encrypted with identity-based encryption. This process involves a procedure called cut-and-choose. The half of the encrypted random scalars are randomly revealed (using a hash function as randomness oracle) as a proof that there is a high chance that at least one of the still hidden signatures has been correctly encrypted. However, this method involves heavy processing for each CET, which can make it challenging to use practically for non-custodial trading. For those who are interested, an annex at the end of this post features more details.

Nevertheless, BLS signatures are appealing due to their lack of a nonce, making oracles stateless without the need to announce or store any information. Furthermore, they allow for easy oracle aggregation, thanks to the mathematical bilinearity provided by pairings and being nonceless.

However, there are still some unresolved issues with this proposal. Firstly, it requires the implementation of a new elliptic curve. Although there are existing reference implementations of BLS curve cryptography, reaching a consensus on which reference implementation to use is necessary. The security of elliptic curves with pairings is still not so well-understood. The protocols utilizing pairings are based on the assumption that the Decision Diffie-Hellman problem is easy while the Computational Diffie-Hellman problem is hard. Recent developments by May and al. 2023 have shown that Computational Diffie-Hellman can be practically reduced to discrete logarithm for many elliptic curves, which implies that solving the computational problem may not be so easy just because the decision problem is easy.

The second issue is the heavy computational burden of the cut-and-choose procedure. Setting up the contract quickly enough in practice for widespread adoption of this scheme might be challenging. However, there are potential ways to improve the computation of proofs and find trade-offs within the DLC setup to reduce the overall computation time.

This solution may be adopted in the distant future, but it remains uncertain. Lloyd Fournier, who is actively working on it, certainly has a better grasp of the timeline and feasibility.

Conclusion on DLC cryptography

Since Dryja's initial proposal for DLC (Discreet Log Contracts), significant progress has been made in refining the protocols. The introduction of adaptor signatures has greatly improved the efficiency by eliminating the need for an extra transaction during settlement. However, the fundamental concept put forth by Dryja remains intact: the utilization of Schnorr's signature for deriving public and private keys during announcement and attestation.

While advancements have been made in this area, the current DLC specifications still adhere to the original concept. However, the future of DLC may not necessarily rely solely on DLC itself. Llyold Fournier's ObC payments (Oracle Based Conditional payments) proposal, which has gained traction in the community, presents compelling possibilities. It introduces stateless oracles that can be aggregated, expanding the oracle community while minimizing computational requirements for users. This proposal offers promising prospects, although it is still being explored.

Although we have explored examples of DLCs with binary outcomes and "winner-takes-all" payouts, we must acknowledge that trading derivatives involves a broader range of payouts. These payouts redistribute funds between the two parties in various ways, depending on the outcome, often represented by a numerical quantity such as a price. In our upcoming post, we will delve into how we can optimize the negotiation and reduce the number of CETs (Contract Execution Transactions) that need to be presigned when an oracle attests a numerical quantity, particularly in the context of price-related scenarios.

And if you want more illustrated details on the BLS based DLCs protocol, here you go:

Annex: BLS based ObC payments

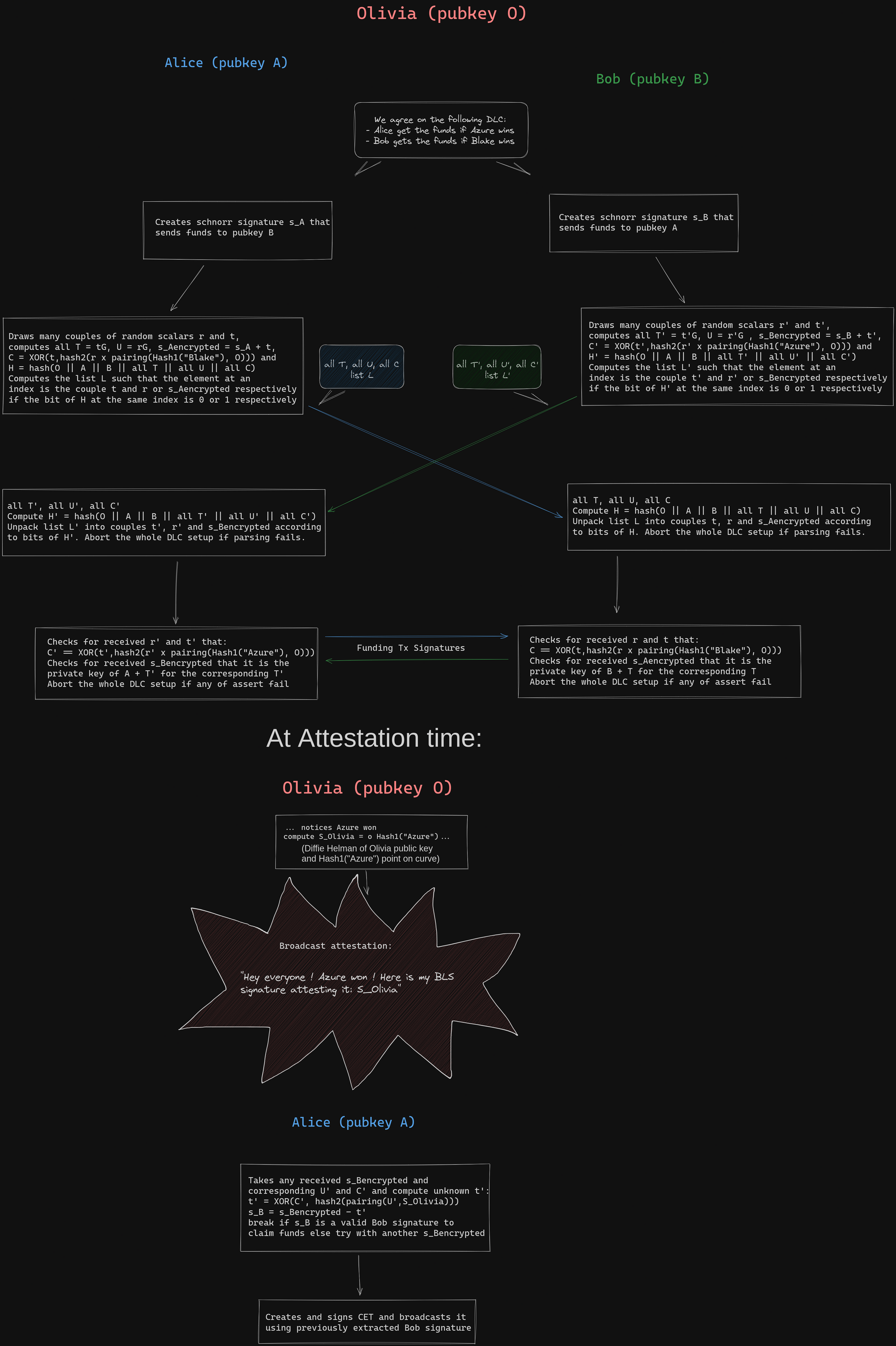
For those who wants to try to grasp the core idea of the BLS based setup of DLCs, here is a full picture of it with some hints to read the details:

• A BLS curve is in fact using two curves: the base curve where points are public keys generated from the addition of a generator with itself as a usual elliptic curve, and the curve where the BLS pairing is valued. The pairing is bilinear and non degenerate so it can be seen as a form of "product"of public keys on the base curve, but the result of this product is not a point on the base curve but on another one.
• Hash1 is a hash to curve function, the resulting hash is a point on the base BLS curve, not a number (hence the uppercase letter in its name)
• hash2 is a function to generate as many random bits as needed from a point on the curve where the pairing is valued (not the same as the base curve). You can see it as a pseudo random bits generator initialized with a seed given by the result of a pairing.
• The hash function of the public data exchanged until now can be used at any point where the verifier must CHOOSE random values to replace him. In the same way we use the hash function to replace Alice at challenge step of Schnorr's signature, we can use a hash as a way to replace her when choosing what value Bob will reveal, sparing us one more interaction.
• The following property expresses that the key to use to encrypt/decrypt symmetrically the Schnorr's signature's tweak can be computed only from a secret nonce \(r'\) or using Olivia BLS signature of the event "Azure" and allows Alice to claim her funds: \[ r' \times \mathrm{pairing}(Hash1("Azure"), O) \\ = o \times \mathrm{pairing}(Hash1("Azure"), r'G) \\ = \mathrm{pairing}(o \times Hash1("Azure"), U') \\ = \mathrm{pairing}(S_{Olivia},U') \\ \]